
Reguläre Ausdrücke - Wie sie funktionieren und wo sie eingesetzt werden
Viele Programme und Datenbanken bzw. Datenverarbeitungssysteme unterstützen reguläre Ausdrücke, auch bekannt unter regex, regexp und regular expressions. Doch was bedeuten diese regulären Ausdrücke und wie funktionieren sie? Diese Fragen werden hier beantwortet und Sie erfahren, wie sich die Ausdrücke in der Praxis einsetzen lassen.
1. Eine kurze Einführung in reguläre Ausdrücke
1.1 Was sind reguläre Ausdrücke?
Vereinfacht ausgedrückt ist ein regulärer Ausdruck ein Muster für einen Text. Reguläre Ausdrücke werden für verschiedene Zwecke verwendet:
- Um Texte nach einem Muster zu durchsuchen (ggf. auch um Teile zu ersetzen)
- Um einen Text mithilfe eines Musters zu validieren
- Um Informationen innerhalb eines Textes mit einer bestimmten Struktur zu extrahieren
Sicherlich gibt es auch weitere Anwendungszwecke. In der Regel wird aber ein Muster verwendet, um einen Text zu analysieren. Das Muster wird dabei ebenfalls als (normalerweise) kleiner Text bereitgestellt, in dem gewisse Zeichen eine besondere Bedeutung haben.
1.2 Ein einfaches Beispiel für einen regulären Ausdruck
Am einfachsten lässt sich der Anwendungszweck anhand eines Beispiels darstellen. Ein regulärer Ausdruck (und in diesem Sinne das Muster) könnte in etwa wie folgt aussehen:
hallo|hello
Dieser reguläre Ausdruck würde nun sowohl auf “hallo” als auch auf “hello” zutreffen, jedoch nicht auf einen anderen Text, wie beispielsweise “salut”. Über den | Operator kann aber im Muster angegeben werden, welche Möglichkeiten erlaubt sind.
1.3 Die Syntax von regulären Ausdrücken
Es gibt verschiedene Regex-Implementierungen, ausserdem kann die jeweilige Syntax dabei gelegentlich geringfügig abweichen. In diesem Artikel liegt der Fokus auf einige sehr verbreitete Elemente:
| Beispiel | Beschreibung |
|---|---|
| abcdef | Trifft auf den Text “abcdef” zu |
| . | Trifft auf ein beliebiges Zeichen zu |
| . | Trifft auf das Zeichen “.” zu |
| abc|def | Trifft auf den Text “abc” oder “def” zu |
| |abc| | Trifft auf das leere Zeichen oder den Text “abc” zu |
| [a-z0-9] | Trifft auf ein beliebiges Zeichen aus dem Bereich “a-z0-9” zu |
| a? | Trifft auf das Zeichen “a” null- oder einmalig zu |
| a* | Trifft auf das Zeichen “a” null-, ein- oder mehrmals zu |
| a+ | Trifft auf das Zeichen “a” ein- oder mehrmals zu |
| a{2} | Trifft auf das Zeichen “a” genau zweimal zu |
| a{2,4} | Trifft auf das Zeichen “a” zwischen zwei- und viermal zu |
| a{2,} | Trifft auf das Zeichen “a” mindestens zweimal zu |
| a{,2} | Trifft auf das Zeichen “a” höchstens zweimal zu |
| abc+ | Trifft auf den Text “abc” einmal oder mehrmals zu |
| (abc)+ | Trifft auf den Text “abc” mindestens einmal zu |
| ^abc | Trifft auf den Text “abc” zu Beginn einer Zeile zu |
| abc$ | Trifft auf den Text “abc” am Ende einer Zeile zu |
Reguläre Ausdrücke sind normalerweise nicht an den Anfang und das Ende eines Textes gebunden. Das heisst, das Muster durchsucht den gesamten Text nach einem Treffer. Damit der Text genau zutrifft, muss er mit dem ˆ und dem $ Operator verankert werden. Zum Beispiel trifft der Ausdruck ˆ(hallo|hello)$ nur auf die Begriffe “hallo” und “hello” zu, nicht jedoch auf einen längeren Text, der den Begriff “hallo” enthält. Mit dem Muster “hallo|hello” ohne Verankerung würde das Muster auch darauf zutreffen. Die Elemente aus der Tabelle können aufgelistet werden, um sich das Muster so zusammenzustellen, dass es seinen angedachten Zweck erfüllt. Ein Muster ist also in der Lage, mehrere Elemente der Tabelle zu kombinieren. Zum Beispiel kann [abc]+ verwendet werden, um willkürlich aufeinanderfolgende a, b und c zu finden.
2. Funktionsweise von regulären Ausdrücken
Bisher wurde erklärt, was ein regulärer Ausdruck ist. Doch wie funktionieren sie und wie sind sie implementiert?
2.1 Reguläre Ausdrücke als endlicher Automat
Zur Erinnerung: reguläre Ausdrücke werden als Text bereitgestellt. Das macht es sehr einfach, diese Muster auf einer Tastatur einzugeben. Reguläre Ausdrücke können allerdings auch als “endlicher Automat” oder als “Zustandsmaschine” beschrieben und grafisch dargestellt werden, denn jeder reguläre Ausdruck lässt sich in eine Zustandsmaschine umwandeln. Die Umwandlung ist dabei einfach umzusetzen und hilft zu verstehen, wie ein Algorithmus reguläre Ausdrücke anwendet.
Eine Zustandsmaschine für den regulären Ausdruck “hallo|salut” könnte somit folgendermaßen aussehen:
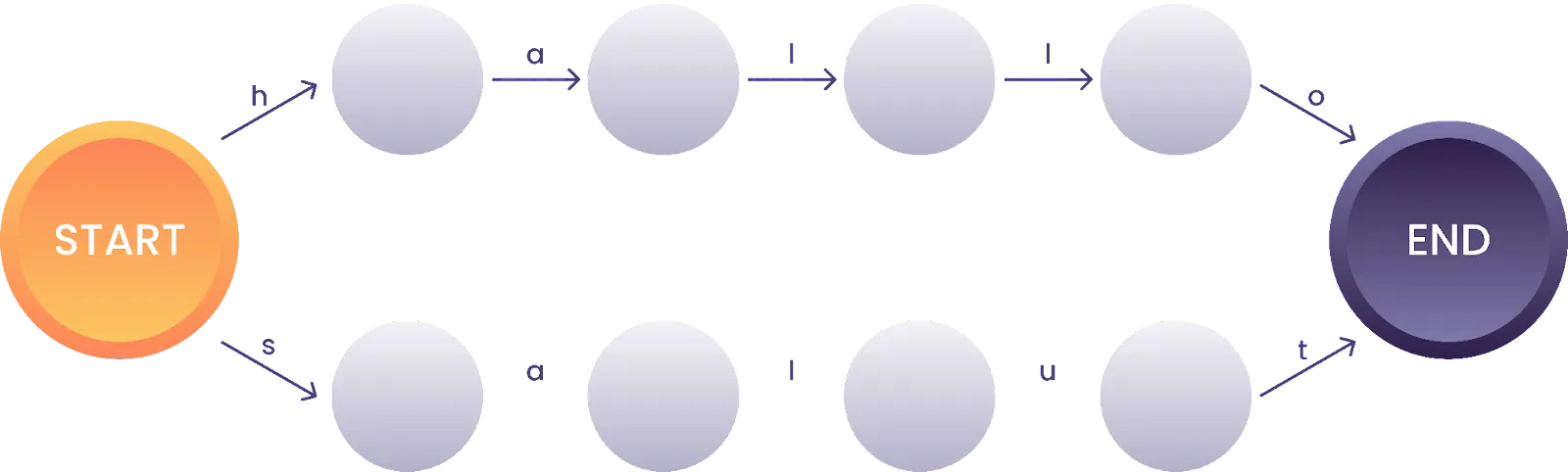 Abbildung 1: Zustandsmaschine für den regulären Ausdruck “hallo|salut”
Abbildung 1: Zustandsmaschine für den regulären Ausdruck “hallo|salut”
Ein Algorithmus startet immer im Anfangszustand “start” und nimmt sich das erste Zeichen von einem zu analysierenden Text, um es mit allen möglichen Zustandsübergängen abzugleichen. Falls kein Zustandsübergang mit dem Zeichen übereinstimmt, liegt an der Stelle kein Treffer vor. Ist dies jedoch der Fall, wird der Vorgang auf Basis des neuen Zustands wiederholt, dieses Mal mit dem zweiten Zeichen. Das Ganze wird so lange fortgeführt, bis entweder kein Treffer oder kein Zustandsübergang gefunden wird oder der Endzustand “end” erreicht ist.
2.2 Zustandsmaschine für Operatoren von regulären Ausdrücken
Die Möglichkeiten, die in einem regulären Ausdruck zur Verfügung stehen, können grundsätzlich in drei verschiedene Kategorien aufgeteilt werden:
- Symbole
- Wiederholung
- Alternation
Einige Implementierungen von regulären Ausdrücken erlauben noch zusätzliche Elemente. Symbole, Wiederholungen und Alternationen werden nachfolgend erläutert.
2.2.1 Symbole als Zustandsmaschine
Mit Symbolen sind Zeichen (Buchstaben, Zahlen, Sonderzeichen etc.) gemeint. Jeder reguläre Ausdruck beinhaltet Zeichen, denn schlussendlich ist es das Ziel eines jeden Ausdrucks, die Symbole mit dem Text abzugleichen. Bei einem Muster “abc” gibt es somit drei aufeinanderfolgende Zeichen, die abgeglichen werden müssen.
Symbole werden in der Zustandsmaschine dagegen ganz einfach als aufeinanderfolgende Zustände dargestellt, mit den jeweiligen Symbolen als Zustandsübergängen.
Das lässt sich am regulären Ausdruck “abc” gut zeigen:
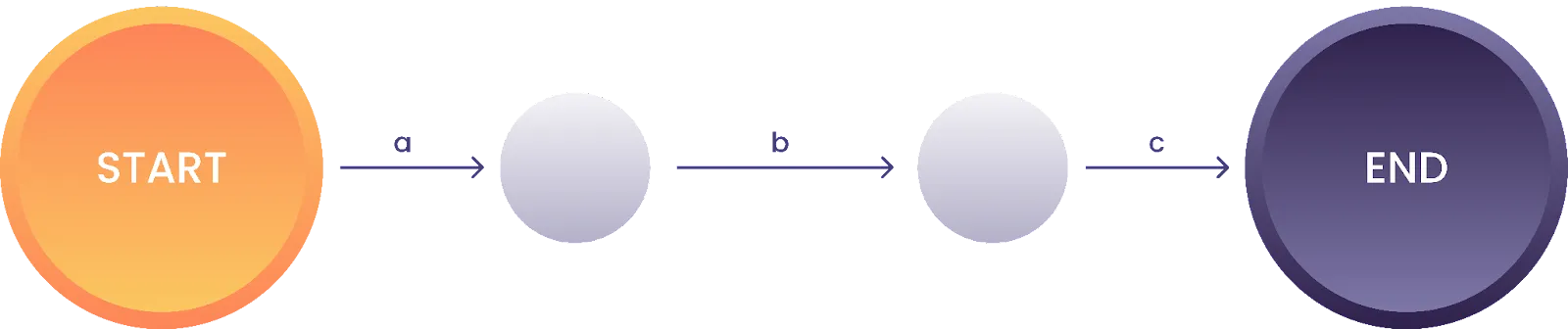 Abbildung 2: Zustandsmaschine für den regulären Ausdruck “abc”
Abbildung 2: Zustandsmaschine für den regulären Ausdruck “abc”
2.2.2 Eine Wiederholung als Zustandsmaschine
Grundsätzlich werden die Operatoren *, + und {a,b} verwendet, um Wiederholungen einzuleiten. Eigentlich können die beiden Operatoren * und + auch mithilfe des {a,b} Operators dargestellt werden. Der * Operator wird dabei für 0 oder mehrere Wiederholungen verwendet. Das lässt sich genauso mit {0,} erreichen. Der + Operator steht für 1 oder mehrere Wiederholungen, was dementsprechend mit {1,} dargestellt werden kann. Es ist in der Praxis tatsächlich aber so, dass diese Elemente sehr oft vorkommen, deshalb sind diese Kurzversionen angenehm, um damit zu arbeiten.
Doch wie sieht eine Zustandsmaschine für eine Wiederholung aus? Als Beispiel dient hier der reguläre Ausdruck (abc)+d (Die Zeichenfolge “abc” ein oder mehrmals aufeinanderfolgend und dann ein “d”):
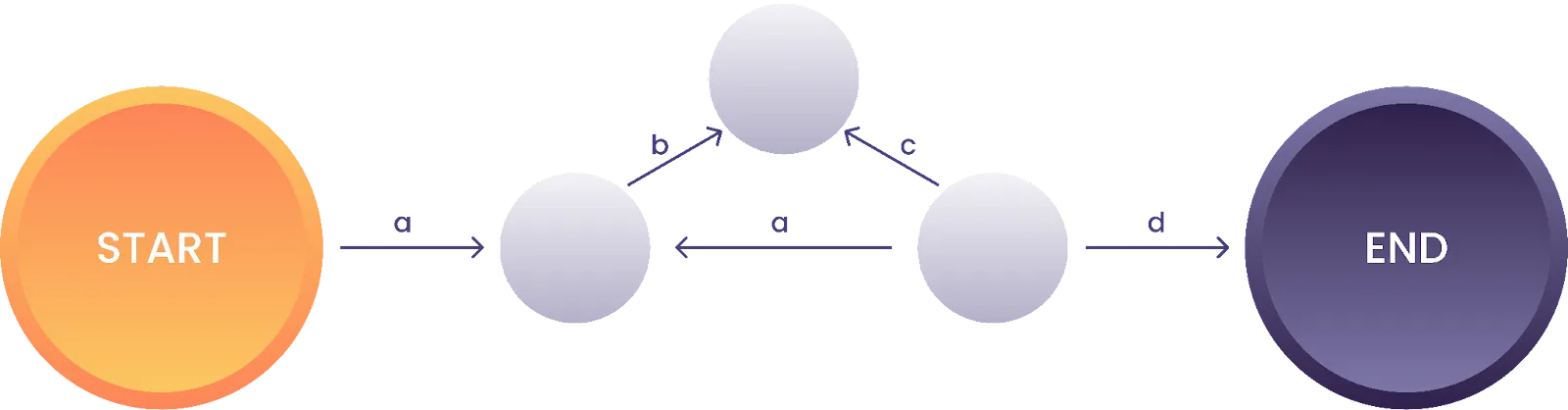 Abbildung 3: Zustandsmaschine für den regulären Ausdruck “(abc)+d"
Abbildung 3: Zustandsmaschine für den regulären Ausdruck “(abc)+d"
2.2.3 Eine Alternation als Zustandsmaschine
Es gibt zwei Arten von Alternationen in einem regulären Ausdruck. Zum einen gibt es die Charakter-Klassen, als Beispiel [abc] und entsprechend einer der Buchstaben “a”, “b” oder “c”. Zum anderen gibt es den | Operator, zum Beispiel abc|def, der den Text in “abc” oder “def” listet. Auch hier kann die erste Variante, die Charakter-Klasse, umgeschrieben werden: a|b|c ist grundsätzlich gleichbedeutend wie [abc].
Zur Verdeutlichung folgt hierzu ein weiteres Beispiel: a[bcd]e:
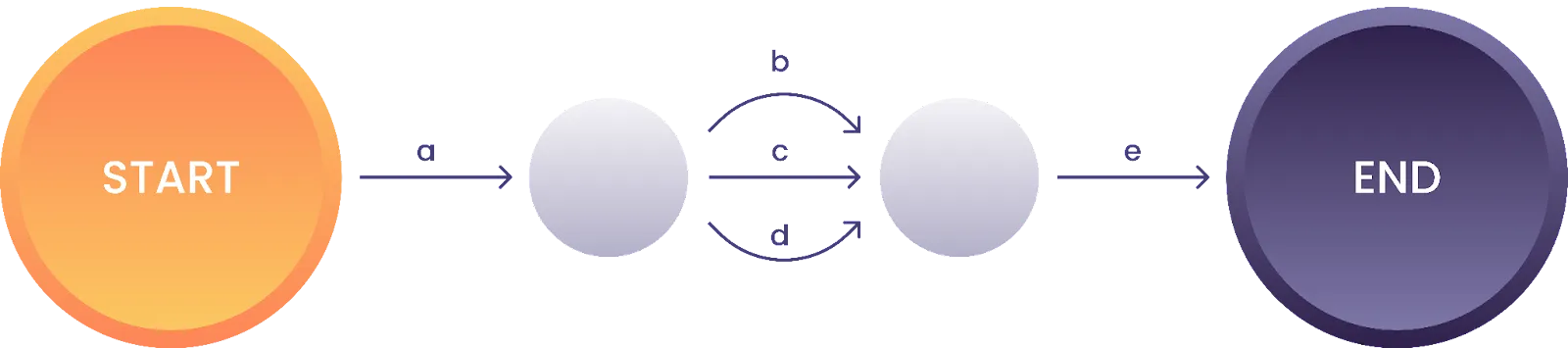 Abbildung 4: Zustandsmaschine für den regulären Ausdruck “a[bcd]e”
Abbildung 4: Zustandsmaschine für den regulären Ausdruck “a[bcd]e”
2.3 Backtracking vs. Non-Backtracking
Es gibt verschiedene Algorithmen für reguläre Ausdrücke. Dabei gibt es hauptsächlich zwei verschiedene Arten, die jeweils Vor- und Nachteilen mitbringen.
Ein Backtracking-Algorithmus testet jeden einzelnen möglichen Pfad eines regulären Ausdrucks so lange, bis ein Treffer gefunden wird. Das ist nicht die effizienteste Lösung, die zur Verfügung steht, bietet aber die Möglichkeit für sogenannte Backreferences (Rückverweise), für die bisher kein effizienter Algorithmus bekannt ist. Wenn eine Implementierung diese Rückverweise implementiert, kann man innerhalb eines regulären Ausdrucks auf vorherige Teile verweisen.
Ein Beispiel: Der reguläre Ausdruck (ab|cd)\1 trifft sowohl auf abab als auch auf cdcd zu, aber nicht auf abcd.
Andere Implementierungen, die nicht auf Backtracking basieren, können viel effizienter sein. Dabei werden nicht alle möglichen Pfäde überprüft, sondern lediglich alle möglichen Zustände.
2.3.1 Effizienz von Backtracking-Algorithmen
Meistens fällt es nicht auf, dass Backtracking-Algorithmen nicht effizient sind. Dazu kommt, dass Backtracking-Algorithmen sehr verbreitet sind, aus dem einfachen Grund, dass sie mehr Möglichkeiten bieten als andere Optionen. Mit dem nachfolgenden Beispiel lässt sich erkennen, welche Folgen das haben kann:
Der einfache reguläre Ausdruck (a|aa)*b, der auf einen bestimmten Text ausgerichtet ist, nimmt einige Zeit in Anspruch, oft liegt diese über einer Minute. Das lässt sich relativ einfach in Chrome und mit JavaScript feststellen:
| |
Ausgabe:
| |
Fazit
Ein einfacher regulärer Ausdruck kann bei Backtracking-Algorithmen zu erheblichen Performance-Problemen führen und diese in die Länge ziehen. Dennoch wird die Methode von vielen Frameworks genutzt: weil sie weit verbreitet sind, es keine schnelle Implementierung gibt oder weil effizientere Methoden schlichtweg nicht bekannt sind. Im Idealfall würde eine Kombination so aussehen, dass die langsame Variante nur genutzt wird, wenn Rückverweise im regulären Ausdruck enthalten sind. Ist das nicht der Fall, würde die effizientere Methode zum Tragen kommen – jedoch käme es hier auch auf den Anwendungszweck an, denn es bestehen durchaus Situationen, in denen es sicherheitskritisch wäre, den zeitintensiveren Weg überhaupt zu unterstützen. Etwa, wenn durch einen Cyber-Angriff mit einem langsamen regulären Ausdruck ein System mutwillig zum Erliegen gebracht wird.
📝 Gefällt dir, was du liest?
Dann lass uns in Kontakt treten! Unser Engineering-Team wird sich so schnell wie möglich bei dir melden.